#Mathsconf31 een terugblik

Op zaterdag 11 maart was er #Mathsconf31 in Bracknell (nabij Londen), tegelijkertijd met #ResearchEdN. Dat leek een lastige keuze te worden, maar met de combinatie van even kort vakantie kunnen houden en er echt even uit zijn is het #MathsConf31 geworden. Een dag lang onderdompelen in met name wiskundedidactiek, weerzien met bekenden van vorig jaar en inspiratie opdoen voor het eigen wiskunde onderwijs.

Wat me in ieder geval op is gevallen, is dat de term Cognitive Load in bijna iedere workshop waar ik aan deelgenomen heb wel op één of andere manier terug kwam. Dat blijkt dus echt wel een ding te zijn waar de (wiskunde) docenten in Engeland mee bezig zijn: hoe kun je wiskunde aanbieden en laten verwerken rekening houdend met een optimale belasting van het werkgeheugen van de leerling. Dat is een interessant maar ook ingewikkelde uitgangspositie bij het ontwikkelen van je lessen, al was het maar dat iedere leerling voor je niet dezelfde werkbelasting zal hebben of ervaren bij dezelfde taak.

Workshop 1 – Phasing learning episodes – Dave Taylor

Dave ken ik voornamelijk van werkbladen die werken volgens het principe van backwards fading en increasingly difficult questions. Vandaag ging het over de structuur van je lessenserie:

In het schema hierboven worden een aantal mogelijke structuren getoond, niet om te pretenderen dat de ene beter is dan de ander, maar wel met een voorkeur van Dave zelf voor de laatste vorm. Op die manier probeert hij nu zijn lessen te structureren. Bij behave moet je overigens denken aan ‘je gedragen als een wiskundige’, het gaat niet om (puber)gedrag en klassenmanagement.

Bij iedere fase Teach, Do, Practice, Behave heeft Dave een slide gemaakt over wat die fasen inhouden en ook wat ze niet zijn (de kracht van voorbeelden en non-voorbeelden daarbij gebruikend).

Dave benadrukt dat Teach geen How-to instructie is. Bij Teach word voorkennis geactiveerd, worden meerdere representaties gebruikt, wordt gemodelleerd (expliciete instructie met afbouw van ondersteuning).

De afwisseling tussen Teach en Do is het ontwikkelen van ‘fluency’ voordat de leerlingen zelfstandig gaan oefenen. In deze fase kun je misvattingen, veel gemaakte fouten e.d. snel waarnemen en op acteren.

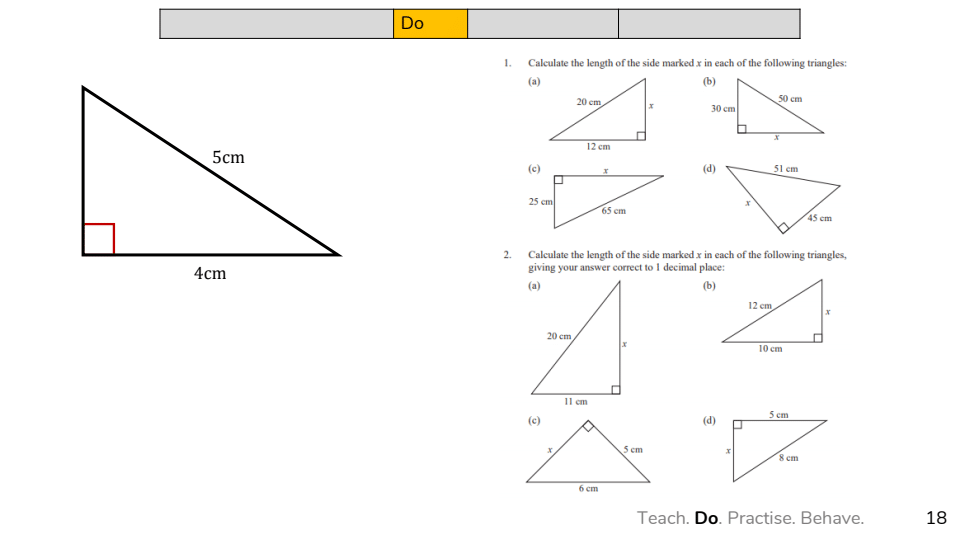
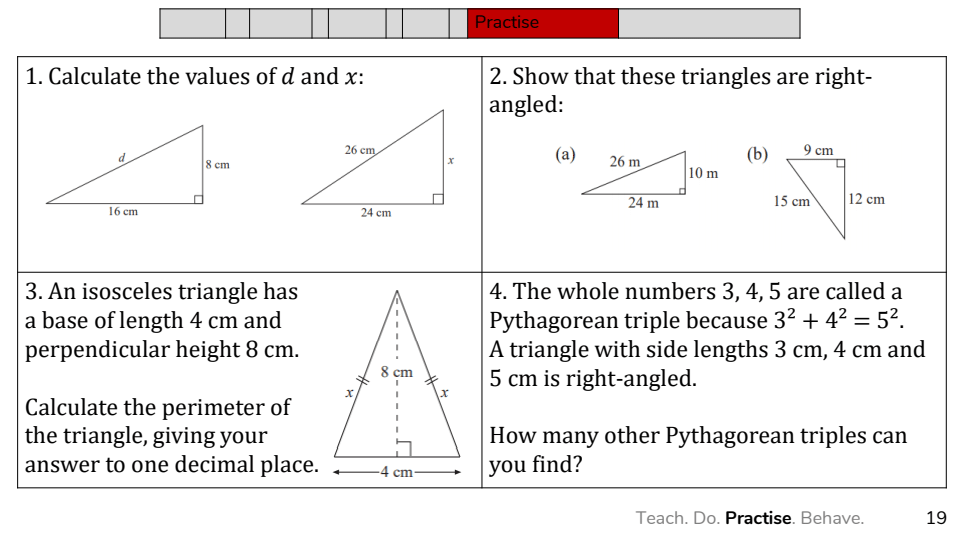
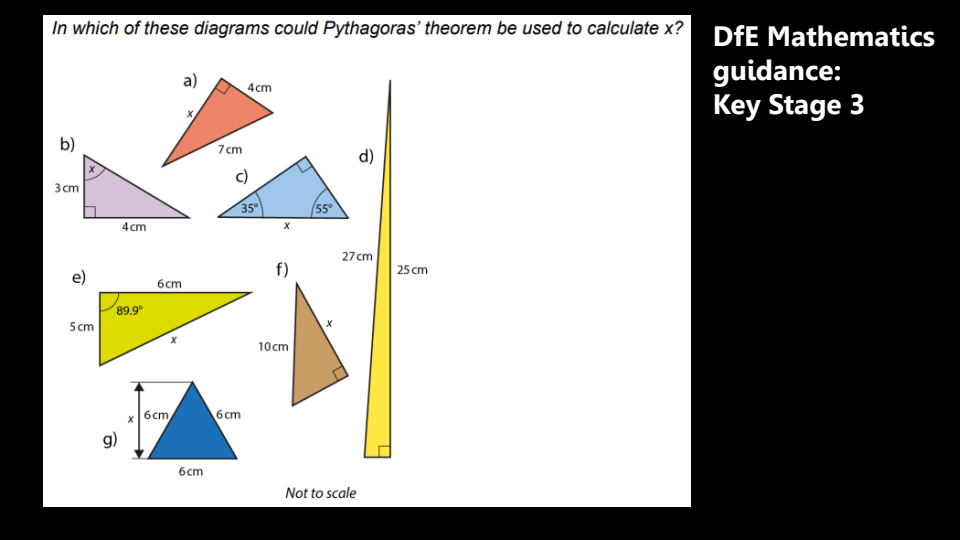
Wat voorbeelden (Pythagoras) voor respectievelijk de fasen Do, Practice en Behave om je een beeld te geven hoe hij dit ziet:

In de Do fase kun je als iets moeilijkheid toevoegen om de overgang van nadoen van de docent / voorbeeld uit het boek naar zelfstandig oefenen wat kleiner te maken.

In de Practice fase ga je verder dan de procedurele kennis en verleg je de aandacht naar meer diepte en (onderliggende) structuren. De leerling moet meer nadenken en meer doen dan alleen maar het stappenplan volgen.

In de Behave fase wil je dat de leerling gaan denken als een wiskundige, ze ook strategieën moeten aanleren om problemen op te lossen of op onderzoek uit te gaan.

De structuur die Dave aanreikt heeft voor mij wel wat parallellen met de learning episode die Craig Barton in zijn boeken heeft geïntroduceerd:

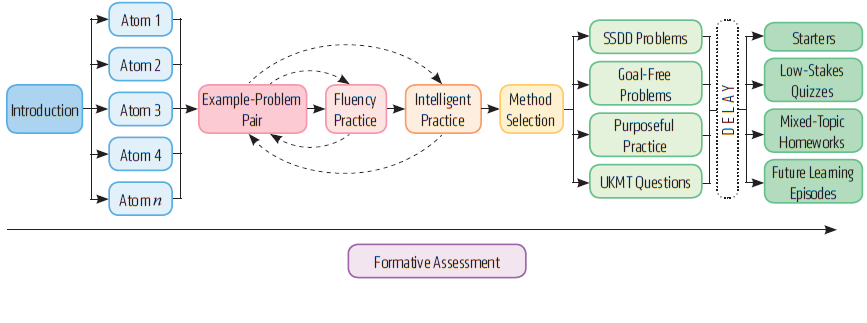
Een uitspraak van Dave die is blijven hangen ging over de, in Engeland, vaak gebruikte ‘I do, we do, you do’ structuur: “Where do you teach?”

Workshop 2 – Putting more challenge into lessons – Adam Mercer

Een volle zaak bij Adam waarin hij ons mee neemt in zijn zoektocht om meer uitdaging te kunnen bieden in lessen. Die uitdaging zat vroege name op het differentiëren in niveau. Opdracht en keuze ruimte bieden aan leerlingen voor eenvoudige, gewone en uitdagende opdrachten. De moeilijkheid zat meestal meer in lastigere getallen en niet in andere vaardigheden, combineren van domeinen of strategie:

Inmiddels heeft hij een andere kijk hierop:

Gedurende de presentatie geeft hij ons zijn 7 regels voor het toevoegen van uitdaging/ challenge aan lessen:

1. Als de hele klas het moet weten of kunnen, dan is het geen challenge;
2. Als het al gemaakt is door iemand anders: gebruik het!;
3. Als je het niet kunt vinden in 10 a 15 minuten: stop zoeken;
4. Als je het zelf maakt: snel en makkelijk en bij voorkeur in powerpoint;
5. Challenge kan op iedere plek / moment in de les;
6. Challenge vervangt niet het doelgerichte oefenen;
7. Vermijd competitie (boek tip: Boys don’t try)

In alle stappen komen allerlei bronnen op internet voorbij met voorbeelden. Een niet volledige lijst met bronnen voor meer dan gewoon ‘worksheets’:

1. goteachmaths.co.uk (betaald)
2. mathshko.com
3. draustinmaths.com
4. interwovenmaths.com
5. mathsvenns.com
6. openmiddle.com
7. Don Stewards blog
8. Corbett’s conundrums

Als je bestaande bronnen gebruikt moet je je wel aan aantal zaken afvragen of op letten:

Varieer in vormen. Iedere les een venndiagram (bijvoorbeeld) haalt niet alleen het plezier en de verrassing weg, het beperkt leerlingen ook tot één manier van denken of aanpak.

Ga na of alle aspecten van de taak relevant zijn voor je leerlingen in de fase van leren waar ze inzitten.

Vanuit cognitive load: ga na of leerlingen alle vereiste kennis en kunde bezitten om de taak succesvol uit te kunnen voeren. Een tip: maak de opdracht eerst zelf en ga na welke voorkennis en vaardigheden vereist zijn. Dit zelf maken geeft ook gelijk de kans om na te denken over welke ondersteuning je wilt bieden en hoe je de opdracht wil introduceren.

Interessante vormen die passeren zijn: Fault it – Fix it, fill in the blanks, always true – sometimes true – never tru, interweaving, doolhof

Workshop 3 – Everybody loves Pythagoras – Jo Morgan

De uitdaging deze workshop was de snelheid van praten van Jo Morgan volgen in het Engels. Geen tijd in mijn hoofd om te vertalen naar het Nederlands.

Net als bij de vorige Mathsconf workshop die ik van Jo heb gevolgd stonden er twee pythagoras puzzels/opgaven klaar voor aanvang om er al even mee te stoeien. Het mooie is dat het je gelijk in het thema brengt:

Er is al zoveel geschreven en gedeeld over Pythagoras dus hoe zou dit nog wat nieuws brengen? Dat is Jo toch weer gelukt. Misschien niet heel schokkend of vernieuwend, maar wat dingen die je wel weet maar die wat minder aan de oppervlakte liggen, waardoor je je er wat minder bewust van bent.

Waarom is Pythagoras toch zo’n geliefd en bekend onderwerp? Behalve dat het in beginsel voor iedereen toegankelijk is, kan het ook heel uitdagend worden (lof floor – high ceiling). Het is een van de eerste stellingen in de wiskunde die leerlingen tegenkomen en waar ze mee aan de slag gaan. Er zit een mooi stuk geschiedenis aan vast (zowel van de stelling als Pythagoras zelf) wat de wiskunde in een andere context zet voor leerlingen. Er is ontzettend veel materiaal beschikbaar voor docenten en leerlingen. Er is visueel veel mee te doen en daarmee ook wat prikkelender en speelser, motiverender voor leerlingen. En door dit alles is het iets waar iedereen wel herinneringen aan overhoudt.

In het wiskunde curriculum is het ook een onderwerp wat op vaker en op meerdere plekken terug komt. Leerlingen komen er dus vaak mee in aanraking en onthouden het daardoor ook veel beter. Het start op jonge leeftijd met de rechthoekige driehoek, maar ook in de latere modules met cirkelvergelijkingen komt dit terug. Op de site van gcsemathsquestions.co.uk kom je bijvoorbeeld deze presentatie tegen met verzamelde pythagoras opgaven (platte vlak) in examens (GCSE’s).

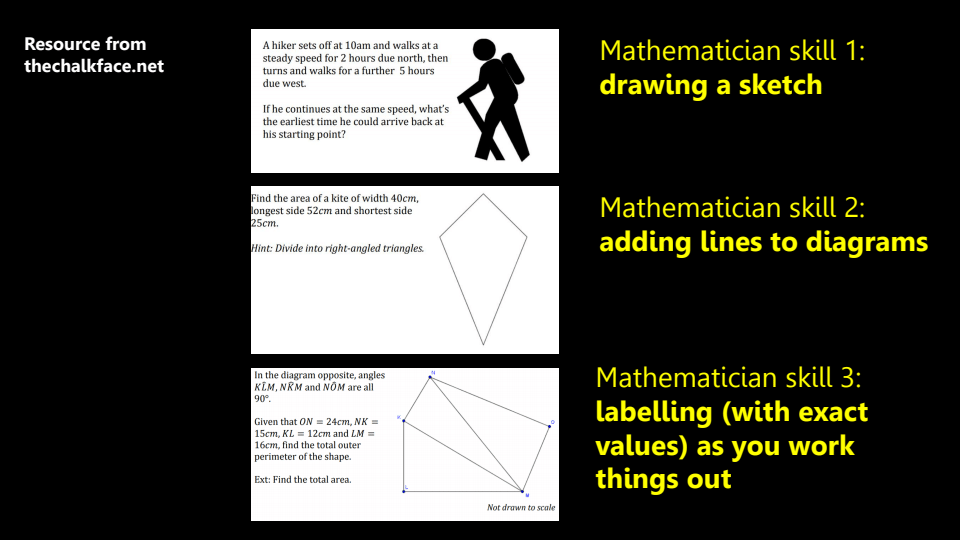
De volgende slide is er zo één waarvan je het wel weet, maar hoe bewust ben je je ervan en hoe bewust geeft je het aandacht in je lessen als afzonderlijke leerdoelen?

Wat heb ik vervolgens gedaan om die eerste vaardigheid wat meer aandacht te geven in mijn 2 havo klas deze week? Ik heb van de site van Amanda Austin een lijst met geschreven ‘situaties’ één voor één getoond en de leerlinge op hun wisbordje (mini white board) de schets erbij laten maken. Geheel in de stijl van Dave : teach – do – teach do etc kon ik heel snel klassikaal feedback geven, aandacht op aspecten leggen etc. In de loop van de opdrachten nam de kwaliteit van de schetsen zienderogen toe.

Een aardige slide om nog te delen, is een overzicht van misvattingen / veel gemaakte fouten:

Een voorlaatste slide die ik nog wel delen is de kwestie van ‘method selection’. Als we met de klas bezig zijn met de stelling van Pythagoras dan moet de leerling in iedere opgave de rechthoekige driehoek vinden en daarop de stelling van pythagoras toepassen. Pas als ze met de goniometrie aan de gang gaan, dan komt de vraag naar boven: gebruik je bij deze opgave de goniometrische verhoudingen of gebruik je de stelling van Pythagoras. Een manier om ze daar al eerder over te laten nadenken in zichtbaar in de slide hieronder. Op de site van Craig Barton’s SSDD problems kun je er overigens nog wel een paar vinden.

De laatste slide die ik wel delen uit deze presentatie is het zelf berekenen van de lengte van de zijden van een Pythagoreaanse driehoek met gehele getallen. Wel leuk om eens zelf uit te proberen.

Workshop 4 – Talk like a mathematician – Lisa Coe

Lisa komt eigenlijk uit het basisonderwijs en is van oorsprong docente Engels.

Dat wiskunde ook een taal is met een eigen structuur, symbolen, woorden, modellen en representaties is geen geheim. Om wiskunde te kunnen gebruiken, toepassen en er over na te kunnen denken moet je beschikken over een juist taalbegrip, horende bij de wiskunde.

Echt begrip van ieder wiskunde concept kan alleen bereikt worden via representaties, abstracties en verbindingen tussen de verschillende representaties.

Een niet wiskundig voorbeeld: wanneer is een dier een hond. Hieronder is niet de slide die Lisa gebruikte, maar ik wed dat iedereen in alle getoonde dieren een hond herkend.

Stel nu ik laat een afbeelding van een paard zien. Hoe weet je dan dat dat geen paard is? Beschrijvende taal is vaak niet toereikend om eenvoudig iets te definiëren (als je probeert de abstractie te maken). Voorbeelden en non-voorbeelden wel. Je gebruikt dan verschillende representaties en de relaties daartussen om tot een juist concept te komen.

We hebben gekeken naar typisch wiskunde vocabulair (Monroe & Panchyshyn, 1995) wat onder te verdelen is in

1. Technisch: alleen gebruikt in de wiskunde, bijvoorbeeld termen als kwadraat, machtsverheffen
2. Sub-technisch: gebruikt in en buiten de wiskunde maar dan wel met een andere betekening, bijvoorbeeld volume (inhoud, geluidssterkte)
3. Generiek: alledaags taalgebruik waarvan de bekendheid afhankelijk is van voorkennis (achtergrond, ervaringen etc), bijvoorbeeld een centrifuge
4. Symbolen: zoals 3, x, : of = die een specifieke betekening in de wiskunde hebben (en mogelijk daarbuiten ook en mogelijk ook anders)

De vraag die Lisa hardop stelt is: moeten leerlingen alle woorden die wij gebruiken in het wiskunde curriculum ook echt allemaal aangeboden worden, en zo ja: voor welke leerlingen is dat dan relevant (nu of later – in verband met het moment waarop je die woorden deelt met leerlingen).
Er ontstond een levendige discussie over woorden als minuend, subrathend en vinculum etc:

Vinculum is in het Nederlands de breukstreep. Ik weet dat Getal & ruimte in de brugklas hier aandacht aan besteed in combinatie met de deelstreep. Je kunt je afvragen of we voor hetzelfde twee woorden moeten hebben. De interessantste discussie vond ik die van de term ‘ongelijkheid’. Moeten leerlingen (op de basisschool, daar lag nu even de aandacht op) al de term ongelijkheid kennen. Iedereen was het er over eens dat ‘kleiner dan’ en ‘groter dan’ concepten zijn die belangrijk zijn om aan te leren inclusief de gebruikte symbolen < en >. Over de symbolen ≤ en  ≥ waren de meningen als iets meer verdeeld. Uiteindelijk waren de meesten het wel eens met het uitgangspunt dat een basisschool leerling het woord ‘omgelijkheid’ niet perse hoeft te kennen als het begrip van het concept groter / kleiner er wel goed in zit.
Noot: Dave Taylor deelde een week ervoor een mooi twitterdraadje over > en < .

Workshop 5 – Approaching a concept coherently – Peter Mattock

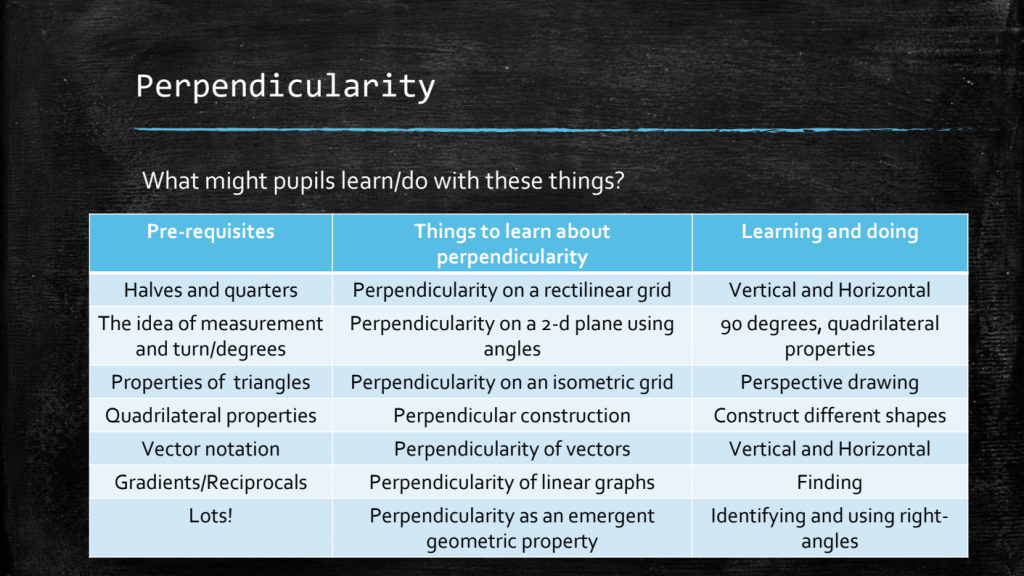
De laatste workshop ronde van de dag. De energie begint wat af te nemen dus ben ik blij dat Peter ons vooral in groepjes laat discussiëren. Aan de hand van Perpendicularity, wat letterlijk haaksheid betekent, maar we houden het maar op het het concept van loodrecht gaan we langs een drietal vragen:

1. Wat wil je dat leerlingen leren over dit concept?
2. Welke voorkennis hebben ze daarbij nodig (in de verschillende fasen waarin ze dit concept uitdiepen)?
3. Wat wil je dat leerlingen er van leren / er mee kunnen doen?

Deze drie vragen helpen je je blik te verplaatsen van ‘Wat moeten de leerlingen nu gaan doen? ” naar “Wat wil ik dat ze hier van leren en wat moeten ze er mee kunnen doen? ” Die shift in gedachten maken, zorgt ervoor dat je anders kunt gaan kijken naar je curriculum, je opbouw erin en het lesmateriaal en vormen die je inzet om leerlingen daar toe te bewegen.

En dan…

Op naar de volgens Mathsconf. Mijn streven is om in oktober weer naar #Mathsconf33 te gaan. De exacte datum heb ik wel voorbij zien komen maar kan ik zo snel nergens terugvinden. Deze staat nog niet aangekondigd op de site van CompleteMaths.

Ik weet wel dat deze in Wakefield is, onder Leeds, dus weer prima te doen met de boot (dan via Hull). Deze keer had ik er met Liesbeth een weekendje London en Windsor aan bast gemaakt. Volgende keer lijkt met me interessant om op donderdag en vrijdag eens met een Engelse wiskunde collega op zijn/haar school een dag mee te lopen.

Dan wil ik ook zelf een korte sessie geven waarin ik aan onze Britse collega’s vertel en laat zien hoe het wiskunde onderwijs in Nederland er uit ziet en georganiseerd is. Dat was eigenlijk al mijn plan voor deze keer, maar daar was ik niet aan toegekomen.

Last but not least: Thanks Julia (@Tessmaths) for driving me and my wife Liesbeth back towards Colchester (near Harwich) on saturday evening!)

De leerling aan het denken krijgen

In onze sectie hebben we eind vorig schooljaar besloten om werk te gaan maken van onze ontwikkeling op het gebied van vakdidactiek. Het handvat dat we gekozen hebben is ‘Volgens Barton‘. Boeken zijn aangeschaft en we zijn begonnen met lezen. Al snel bleek dat er wel heel veel in deze boeken staat waar je mee aan de slag kunt gaan. Uit een eerste schifting kwam de hoofdstukken 4, 6 en 7 als favoriet boven drijven. Deze gaan respectievelijk over ‘Het denken richten’, ‘Uitgewerkte voorbeelden’ en ‘Keuze van voorbeelden en oefenvragen’.

In een vervolg stap heb ik van ieder hoofdstuk een bundeling van de kern ervan gemaakt en hieruit hebben we uiteindelijk hoofdstuk 4, ‘Het denken richten’ gekozen. Het thema dat we voor onszelf benoemd hebben is “Hoe zet je de leerling aan het denken?”.

We zijn het er binnen de sectie allemaal over eens dat:

• de leerlingen veel focussen op vaardigheden en reproductie;
• dat voor een deel voort komt uit de periode van onderwijs op afstand, waarin wijzelf ook de nadruk daar wat meer op gelegd hebben;
• leerlingen veel consumentengedrag laten zien; het lijkt ze te moeten komen aanwaaien en als het niet gelijk lukt wordt snel de handdoek in de ring gegooid;
• leerlingen denken lastig vinden, en dat is het ook. Dus hoe kunnen we daarvoor de juiste didactiek bij vinden?
• het denken van leerlingen binnen ons vak juist zorgt voor diepere kennis en meer betekenis. Het tilt het vak op van een kunstje doen, naar wiskunde gebruiken/toepassen/bedrijven om de wereld om je heen te leren begrijpen.

Ontwikkeldagen

We hebben als sectie een aantal ontwikkel dagen/dagdelen in de jaarkalender. Op de eerste ervan heb ik een korte masterclass gegeven over de werking van het geheugen, belang van voorkennis, cognitieve load, silent teacher en doelvrije opgaven.

We hebben daaruit allemaal een element gekozen om alleen of met iemand samen daarvan iets uit te proberen en toe te passen in een of meerdere lessen.

De tweede studiedag was vorige week en ik vroeg me af wat een goede manier was om deze bijeenkomst te starten, met als doel een effectief vervolg te geven aan waar we mee gestart zijn.

Nu kwamen er de afgelopen twee weken verschillende bronnen voorbij die hier allemaal bij aanhaakten. De vraag is of dat toeval is, of dat ik me bewuster was van wat ik voorbij zag komen omdat ik de bril van ‘de denkende leerling’ op had. Ik vermoed dat laatste.

Deze bronnen zijn:

Een blog van Doug Lemov met daarin een poster van Innerdrive.

Een podcast van Beyond Survival (Jamie Thom) met Tom Sherrington over vragenstellen in de les

Het boek Slow teaching van Jamie Thom, met name ook het hoofdstuk 6 over Vragenstellen en wachttijd.

De start van de tweede ontwikkeldag

Mijn start was als volgt:

‘Fahimeh, welke werkvormen die we gehad hebben in de vorige bijeenkomst kun jij je nog herinneren?’

‘Oh, ik heb je vraag gemist, wil je die herhalen?’

‘Zeker, ik vroeg welke werkvormen die we gehad hebben in de vorige bijeenkomst kun jij je nog herinneren?’

‘We hebben het gehad over hoe belangrijk het activeren van voorkennis is, omdat je met actieve voorkennis…….’ (Het antwoord liep nog wat langer door).

‘Jort, kun jij nog aanvullen?

‘Silent teacher.’

‘Dat is zo, en ook naar doelvrije opgaven hebben we gekeken.’

Hierna volgde een tweede vraag:

‘Even een vraag om allemaal over na te denken. In het overzicht van hoe Barton een lessenserie ziet, benoemt hij drie vormen van oefenen. Denk even na welke drie dat waren’.

Na ongeveer 15 seconden liet ik het overzicht zien, met daarin de drie vormen afgedekt, maar wel zichtbaar waar deze qua positie zitten in de lessenserie.

Na nog 15 seconden: ‘Wissel uit met degene naast je, waar komen jullie samen op uit?’

Gevolgd door daarna een klassikale uitwisseling en het volledige plaatje met een korte schets van de inhoud van de drie vormen.

De derde vraag die ik gesteld heb was met wisbordjes. Geleend van Doorloopjes heb ik de volgende afbeelding en vraag laten zien. Dit hebben ze nagetekend en aangevuld.

Na 3 -2 -1 steek je bordje maar op hebben we uitgewisseld en heb ik het plaatje laten zien, die we in de vorige bijeenkomst gebruik hebben.

Vragen stellen

Waarom deze drie soorten vragen? Omdat ik hierna aan mijn collega’s de volgende vragen heb gesteld:

• Bij welke vorm werd je zelf het meest geprikkeld tot nadenken?
• Bij welke vorm was je het actiefste ?
• Van welke ga je – verwacht je – het meest onthouden?

We willen namelijk de leerling aan het denken zetten. En dat kan ook al heel eenvoudig, zonder veel voorbereiding van perfecte werkbladen, presentaties of opdrachten. Dat begint al in de les, hoe je leerlingen bevraagt en hoeveel wachttijd je inbouwt.

Dat laat de volgende poster van Innerdrive mooi zien:

Vragen stellen……. en wachten

In een vraag gestuurd gesprek met de klas moet je doel zijn om alle leerlingen aan het denken te krijgen. Uit onderzoeken weten we inmiddels dat multitasken (meerdere cognitief belastende activiteiten tegelijkertijd doen) niet bestaat. Alleen dat waar je de aandacht op richt vult het (werk) geheugen. Als je leerlingen dus niet activeert om na te denken over de vraag die je stelt, heb je geen zicht of verdere invloed op wat er in het hoofd afspeelt. Alle leerlingen daarom actief betrekken bij je vraag vergroot de kans voor iedere leerling om dat ook te doen!
In het voorbeeld uit mijn gesprek met met collega’s is duidelijk dat als je eerst een naam noemt en dan pas de vraag stelt, de anderen in de klas zich niet aangesproken voelen. Een deel zal misschien wel ook nadenken over de vraag die gaat komen, maar zeker niet iedereen, je bent of voelt je immers niet aangesproken. Ondanks dat ik dit weet, trap ik hier nog wel eens in omdat ik een bepaalde vaart in de les of in het gesprek wil houden. Maar feitelijk ontneem ik dan kansen bij leerlingen.

Dus eerst de vraag stellen en dan pas een naam noemen. Niet met vingers omhoog werken, is dan het devies, want wie zijn vinger niet opsteekt hoeft dan blijkbaar ook niet te denken. En de kans is groot dat de leerling die het weet zijn hand opsteekt, dat is sowieso een slechte graadmeter voor jou om na te gaan of ‘de klas’ dit weet. Tom Sherrington geeft in de podcast nog praktische adviezen over hoe je om gaat met die betrokken en enthousiaste leerling die graag wil laten horen dat hij/zij het weet.

Na het stellen van de vraag wacht je even om een naam te noemen. Leerlingen moet wel denktijd hebben om je vraag te horen, te decoderen wat je eigenlijk van ze vraagt, na te gaan wat ze er van weten (ophalen uit hun lange termijn geheugen) en hun antwoord alvast in hun gedachten te formuleren.

Jamie Thom weidt in zijn boek op pagina 67 ook nog een bladzijde aan de (welbekende) reactie ‘geen idee’ als antwoord van een leerling. Deze leerling mag daar niet mee wegkomen, want als je dit toestaat promoot je eigenlijk dat dit oke is. Terwijl deze leerling in de meeste gevallen gewoon (nog) niet heeft nagedacht of de vraag niet goed heeft gehoord of begrepen. Doug Lemov noemt dit ‘no opt out’.

Bij de toevoeging van het wisbordje voelden mijn collega’s iets meer druk om iets op te schrijven. ‘want mijn bordje mag natuurlijk niet leeg blijven’. Er werd harder nagedacht, maar het miste even de uitwisseling en het completer maken van hun begrip / antwoord. De voordeel van de wisbordjes voor de docent is dat je heel snel van iedere leerling ‘het denken zichtbaar krijgt’.

Wachten is dus een hele simpele interventie om meer leerlingen aan het denken te krijgen. Het kost je geen extra voorbereidingstijd, maar is in de uitvoering misschien lastiger (wachten lijkt altijd langer te duren dan het in werkelijkheid is).

Het vervolg van onze tweede ontwikkeldag

Na het gezamenlijke deel ben ik met twee collega’s die ook lesgeven in de 2 havo jaarlaag aan de slag gegaan met het maken van doelvrije opgaven bij het komende hoofdstuk over lineaire verbanden (grafiek tekenen bij een formule, een lineaire formule opstellen bij een verhaal/tabel/grafiek en het opstellen en oplossen van lineaire vergelijkingen).

We zijn het gewoon om een heel specifiek resultaat te vragen bij een opgave: teken de grafiek bij… , los de vergelijking op, bereken het snijpunt, geef de formule van.. et cetera.

Een doelvrije opgave kenmerkt zich door het open karakter van de vraag. Er wordt een situatie beschreven of gegevens in één of andere vorm gepresenteerd en de vraag komt dan eigenlijk neer op : Wat kun je uit deze gegevens berekenen, tekenen,
opstellen, beredeneren en concluderen?

Zo’n opgave helpt bij het ontwikkelen van een onderzoekende houding, het zorgt ook voor het goed kijken naar de gegeven data en om dat te koppelen aan wat je in je lange termijn geheugen hebt zitten. Het leert leerlingen ook te beginnen aan een opgave. We zien toch vaak dat leerlingen naar een opgave kunnen staren en omdat ze niet gelijk de hele route naar het antwoord kunnen zien, dan ook maar niet beginnen. Wij stellen dan vaak de vraag: ‘Wat herken je wel, of wat zou je wel kunnen?’
Doelvrije opdrachten kennen dan ook niet zo zeer een goed of fout antwoord, daarmee is het een opdracht met een lage drempel en een hoog plafond. Daarmee bedoel ik: iedereen kan instappen, het is laagdrempelig want er is altijd wel iets wat je kunt. En het hoge plafond is dat je qua uitdaging vaak ook verder kunt gaan dan misschien op dat moment van je gevraagd zou (kunnen) worden. Succes voor iedereen en uitdaging die past bij iedere leerling.

Een Engelstalige blog met doelvrije opgaven bij wiskunde is http://goalfreeproblems.blogspot.com/.

Een doelvrije opgave kan zo simpel zijn als:

Klik op de afbeelding om de powerpoint met de vragen van dit hoofdstuk te downloaden.

Wat je hier zoal al mee kunt?

• benoemen dat dit lineaire formules zijn;
• dat er één stijgend en één dalend is;
• dat er één de positieve y-as snijdt in (0,8) en de andere de negatieve y-as in (0,-17);
• je kunt tabellen maken;
• je kunt de grafieken tekenen;
• je kunt uit tabel en grafiek het snijpunt bepalen;
• je kunt een vergelijking opstellen;
• je kunt die vergelijking oplossen en het snijpunt berekenen;
• je kunt een verhaal/context bedenken bij de formules;
• …

Het is wel aan te bevelen om zelf als docent eerst zo’n overzicht helder te hebben voor jezelf, van wat je van leerlingen verwacht. Dat kan helpen bij het gericht vragen stellen. Maar het is ook goed om niet te veel te sturen en je te laten verrassen door wat leerlingen eruit halen.

Duurt zo’n opdracht dan niet lang? Dat kan, zeker als je ergens toch hoopt of verwacht dat ze alles eruit halen wat er in zit. Maar is het dan wel doelvrij? Is dat je bedoeling? Ik zie het meer als training in leren aanpakken & in leren ophalen uit je geheugen. Daar kun je ze 10 minuten voor geven. Maar ook 20 minuten of een hele les. Ik noem daarbij een deel van de les, want zeker als je hier mee start lijkt zo’n opdracht als huiswerk me niet passend. Daar is niemand die kan stimuleren door de juiste vragen te stellen, wie helpt hen doorzetten?

Ik kijk uit om de ervaringen hiermee straks met mijn collega’s uit te wisselen en samen een stapje verder te komen in het leerlingen nog meer aan het nadenken te krijgen bij wiskunde.

Noot: Deze blog is in korte tijd geschreven, met name voor mijn eigen leerproces. Her en der zal er wellicht een typefout of spelfout in zitten. Mocht je een storende fout zien, laat het me weten, dan haal ik die er uit.

Workshop Craig Barton 7 jun 2022

We hebben er als deelnemers even op moeten wachten, het oorspronkelijke plan was in het jaar 2020, maar afgelopen 7 juni was het dan toch zo ver: Craig Barton was in Nederlands voor het geven van een workshop.

Voor wie Craig Barton niet kent: Craig heeft inmiddels twee boeken geschreven How I wish I’d taught maths en Reflect, Expect, Check, Explain. De eerste is vertaald naar het Nederlands door René Kneyber en dat boek wordt inmiddels ook veel gebruik in docentopleidingen. Als er in Nederlands over het tweede boek van Craig gesproken wordt dan wordt vaak deel 2 van de vertaling van het eerste boek van hem bedoeld. Deze is namelijk in twee delen gepubliceerd (en inmiddels ook als één boek te verkrijgen). Naast de twee genoemde boeken heeft Craig ook een aantal websites (diagnostic questions, variation theory, SSDD problems, Maths Venns) in beheer en heeft hij zowat iedereen die iets aan onderwijsonderzoek gedaan heeft in zijn podcast gehad.

De workshop van 7 juni heeft als titel meegekregen: Explanations, modelling and Worked Examples.

Dat Craig veel reflecteert en dat ook belangrijk vindt, weten lezers van zijn 2e boek inmiddels vrij goed. Hij start dan ook met de slide:

Kortom: neem niet alles klakkeloos over maar probeer steeds de vertaling te maken naar jouw eigen situaties en maak het zo concreet mogelijk.

Voorkennis

We worden gelijk aan de slag gezet om een onderwerp te kiezen die we binnenkort in de les gaan introduceren. Vervolgens worden we uitgedaagd om alle benodigde voorkennis die een leerling daarvoor moet hebben op te schrijven en uit te wisselen met de collega naast ons.

Als je daar goed over nadenkt dan is dat vaak heel veel. Zo laat hij zien welke voorkennis relevant is voor het leren bereken van de oppervlakte van een cirkel:

Het belang van de voorkennis is tweeledig. Nieuwe informatie sla je op door het te koppelen aan bestaande informatie. Voorkennis activeren zorgt er voor dat er voldoende haakjes ontstaan waar de leerling wat gaat komen aan kan koppelen / ophangen. Een tweede functie zit in de (ongewenste) belasting van het werkgeheugen. Als delen van de voorkennis nog niet goed in het systeem of geheugen van de leerling zit, dan levert dat een extra, en op dat moment ongewenste, belasting op van het werkgeheugen. Omdat het werkgeheugen beperkt in capaciteit is, blijft er minder ruimte over voor het leren van de nieuwe kennis of vaardigheid. Daar voeg ik dan zelf nog aan toe dat dit ook iets doet met de modus (leerstand) van de leerling: het nieuwe wordt onnodig als moeilijk bestempeld en de leerling haakt al heel snel weer af. Succes op vereiste voorkennis creëren geeft de leerling ook weer wat zelfvertrouwen voor de volgende stap.

Het is natuurlijk niet te doen om alle voorkennis te controleren. De tip van Craig is om de voorkennis te prioriteren en alleen te kiezen voor de essentiële voorkennis, zonder welke de leerling echt niet verder zou kunnen nu. Alleen die delen van de voorkennis controleren je actief in je les. Hier zit de kunst van het weglaten in en leun je op de ervaringen die je hebt: alles is belangrijk, maar waar zitten de struikelblokken?

Voorkennis activeren moet snel kunnen, iedereen moet reageren en je moet voorbereiden hoe je wilt reageren op wat je gaat waarnemen: voorbeelden te geven, leerlingen met elkaar laten uitwisselen en indien nodig kun je ook iets opnieuw uitleggen.

Beslissingen nemen

Nu weet ik niet precies wat de brug naar dit onderwerp was, maar we hebben stilgestaan bij het nemen van beslissingen. Iets wat wij als experts vaak onbewust en automatisch doen, maar wat niet in de werkwijze of systeem van leerlingen vanzelf of bewust gebeurt. Daarom de tip: onderwijs het nemen van beslissingen apart. Beslissen of je antwoord compleet is, beslissen of de breuk volledig vereenvoudigd is, beslissen of iets een vergelijking is, beslissen of je moet optellen of aftrekken bij een stelsel van vergelijkingen: wij als experts denken daar niet meer over na: de vloek van kennis komt voorbij!

Het onderwijzen van het nemen van beslissingen bestaat uit twee stappen volgens Craig: het identificeren van te nemen beslissingen en het nemen van de beslissing zelf.

We passen dit toe op het onderwerp dat we eerder zelf hebben gekozen aan het begin van de workshop (dit eigen onderwerp komt steeds terug, zodat we wat Craig ons laat zien vertelt, steeds actief verwerken en vertalen naar onze eigen praktijk). Ik had gekozen:

Los op: -8a²+2a = 4a

Wat een leerling hier moet beslissen is:

• Dit is een vergelijking
• Het is een kwadratische vergelijking
• Het is een tweeterm
• Een tweeterm ontbind je met enkele haakjes
• Ik moet eerst op 0 herleiden

Kijkend naar de eerstgenoemde beslissing, voor veel leerlingen gelijk een lastige: wat is een vergelijking en hoe herken ik die?

Is 2 + 3 = 5 een vergelijking?

En 2a + 3 = 5?

Of 5 = 2a + 3

En is de vergelijking een kwadratische vergelijking?

Bijvoorbeeld 2² + a = 7

En 2 + a² = 7

En deze 2a + a² = a² + 7

Bij het identificeren is het werken met voorbeelden en non-voorbeelden heel krachtig. Ook het opzoeken van de grensgevallen (boundary examples) draagt bij aan een sterk conceptueel begrip. Door steeds een kleine verandering toe te passen kunnen leerlingen focussen op de specifieke kenmerken die jij steeds aan geeft. Daar zit een kern van de variatietheorie achter:

Voorbeelden kiezen (voorkennis en nieuwe kennis)

Het kiezen van goede voorbeelden vraagt een gedegen voorbereiding, want welke (non) voorbeelden en grensgevallen ga je kiezen, waar wil je dat ze over nadenken, waar zitten de misvattingen? De voorbeelden mogen niet te makkelijk, maar ook zeker niet te moeilijk zijn: de eerste ervaring moet positief zijn en de voorbeelden moeten tot denken aanzetten. De voorbeelden moeten ook niet leiden tot verkeerde generalisaties waarbij de leerling met een verkeerde aanpak of foute kennis toch tot het juiste antwoord komen.

Slechte voorbeelden daarvan zijn:

• 2²
• 10% van 70
• Bij een rechthoek met zijden 3 en 6 de oppervlakte vragen
• Het gemiddelde vragen van 5 6 8 9 12
• De breuk 16/64 vereenvoudigen

Zie het einde van dit blog om te zien waarom deze voorbeelden niet goed zijn.

Verdere tips bij het kiezen van voorbeelden zijn het voorkomen van terugkerende getallen of elementen in je voorbeelden en niet te veel tegelijk in één voorbeeld proppen: maak een keuze, breng focus aan. Gebruik een aantal gerelateerde voorbeelden (doel: verbindingen leggen) en als je rijtjes maakt met steeds een klein verschil, reset dan na een aantal voorbeelden; begin een nieuw rijtje.

Self explanation – uitleggen aan jezelf

We gaan verder met de leerstrategie: uitleggen aan jezelf.

Uit onderzoek blijkt dat de best presterende leerlingen (ongeveer 20% van de leerlingen) dit vanzelf doen. Leerlingen die dit doen kunnen makkelijker problemen oplossen. Gelukkig is dit een vaardigheid of leerstrategie die aangeleerd kan worden.

Luistertips over dit onderwerp zijn te horen bij concurrent / collega podcaster Ollie Lovell in zijn ERRR podcast #044 met Alexander Renkl en podcast #060 met Anita Archer.

Het aanleren van deze strategie kun je ondersteunen door op bepaalde momenten vragen te stellen die het denken richten. Zoals: Wat gebeurt er nu? Wat heb ik net gedaan? Wat denk je dat er nu volgt? Klopte je verwachting, wat was er anders en waarom? Het tweede boek van Craig heet niet voor niets Reflect, Expect, Check, Explain bedenk ik me nu. Door met behulp van deze vragen de leerling te laten nadenken gaat de leerling verbindingen leggen tussen het specifieke voorbeeld en de generieke regel. De prompts (aanwijzingen en vragen) die je geeft zijn generiek van aard (dus niet specifiek gericht op getallen of elementen uit het voorbeeld) om die generalisatie te kunnen maken.

Voorbeelden:

Hoe laat je leerlingen op deze vragen reageren? Een aantal suggesties:

Nadenken is iets wat leerlingen lastig vinden om te doen. In een lessituatie waarin de docent aan het uitleggen is (leerling: luisteren), noties maakt op het bord (leerling: lezen) en denkvragen stelt (leerling: in zichzelf moet praten) ontstaat een overbelasting bij de leerling: luisteren en lezen moeten door hetzelfde deel van je hersenen gedaan worden. In jezelf nadenken is praten tegen jezelf (taal!): ook weer zelfde deel van je hersenen wat aan de slag moet. Je zou dus tijd voor iedere stukje apart tijd moeten geven.

Silent teacher en Narration

In de voorbeelden hierboven met de worked examples, zie je twee van de drie kolommen die Craig hierbij gebruikt. Aan de linkerkant werkt hij in stilte het voorbeeld uit. Daarna komen de denk vragen (één voor één) en na afloop wordt nog een keer een heel voorbeeld in zijn geheel gedaan (de kolom aan de rechterkant die niet in de afgebeelde voorbeelden te zien is). Tijdens silent teacher mogen leerlingen alleen kijken en luisteren (niet schrijven of praten dus) om de aandacht volledig te kunnen focussen. Is het een lang voorbeeld dan kun je een stap van de uitleg silent doen, dan de denkvragen stellen en bespreken (het narration deel) om vervolgens weer door de gaan. Bij korte voorbeelden kan dat in één run.

In de eerdergenoemde podcast met Anita Archer worden drie fasen onderscheiden. De I do, We do en You do. Silent teacher zit duidelijk in het I do deel. De denkvragen bespreken zie ik als een brug tussen de I do en de We do omdat we op dat moment nog niet samen een voorbeeld aan het uitwerken zijn. In die fase pak je een nieuw voorbeeld en ga je (ook weer met denkvragen) samen met de leerlingen stap voor stap de uitwerking door. In de You do fase doet de leerling dat alleen.

Nog wat praktische tips bij het bespreken:

• Wat snel kan is klassikaal (choral) een kort antwoord laten geven: je telt af en de klas spreekt tegelijk het antwoord uit
• Mini wisbordjes
• Klassengesprek – Coldcall: niet met vingers opsteken maar random leerlingen aanwijzen en een volgende leerling op de eerste laten reageren
• Klassengesprek – No opt out: ofwel ik weet het niet is niet een einde van het gesprek, altijd bij de leerling terugkomen met een nieuwe of vervolg vraag

En toen was het pauze. Het middag deel van de workshop ging over geheugen en retrieval practice. Daar zat voor mijzelf niet zo heel veel nieuws in. Omdat ik met het schrijven van mijn blogs vooral mijn eigen reflectieproces ondersteun laat ik het middagdeel ook even voor wat het was. Misschien volgt er later nog wel iets, maar ik wil eerst nog de verwerking doen van mijn bezoek aan #Mathsconf29.

Als afsluitend nog een prikkelende vraag die gedurende de ochtend voorbijkwam waar je je eigen gedachten nog eens over kunt laten gaan:

Toelichting bij de slechte voorbeelden:

• 2 x 2 = 4 en 2 + 2 = 4
• Een nul wegstrepen als strategie
• Oppervlakte en omtrek zijn gelijk
• Gemiddelde = mediaan
• De 6 wegstrepen in teller en noemer

#MathsConf29 – eerste overpeinzingen

Tijdens (of beter: dankzij) de Covid lockdowns kreeg de kans om een #MathsConf een keer bij te wonen: online. Daarvoor heb ik het altijd met de twitter draadjes moeten doen. Ik had me voorgenomen om, als het weer live zou zijn, eens een keer te gaan. Vandaag was de tweede fysieke bijeenkomst na de lockdowns en ik ben geweest.

Misschien ga ik er nog een keer wat langer op in, op de verschillende sessie die ik heb bijgewoond en waarom dit echt een toevoeging is aan wat we in Nederland aan wiskunde bijeenkomsten hebben.

Voor nu is dit een poging om mijn eigen ‘take away ‘ helder te krijgen. En dat is even nodig, want ik heb zo veel gehoord en gezien vandaag, dat het een soort overload is aan gedachten en ideeën. Ik heb het gevoel dat er wel een rode draad in zit.

En die rode draad komt wellicht door wat collega Fahimeh in onze sectie bijeenkomst afgelopen week als antwoord gaf op een gestelde vraag: “Hoe krijgen we de leerling aan het denken? ” De vraag was met welk onderwerp we uit de boeken van Craig Barton volgend jaar als sectie gemeenschappelijk gezamenlijk willen starten met onze professionalisering. Specifieker verwees mijn collega nog naar twee hoofdstukken met onderdelen als Silent teacher (met denk prompts) en worked examples (als ik me niet vergis).

Vandaag heb ik een aantal sessies bijgewoond, en per sessie zijn de volgende kernwoorden blijven hangen

Ronde 1: Behaving mathematically: onderzoeken, verwondering, verbazing, denkvragen stellen, patronen herkennen, generaliseren, “My job is not to turn you into calculators, but to make mathematicians ” , wat valt je op. “Thinking mathematically “, op welke andere manieren

Ronde 2: Highly effective teaching: mastery learning (every student), belang van voorkennis helder hebben en dat tijdig op- en aan te pakken; responsive teaching, vak- en pedagogische kennis, cognitieve belasting, planning en fasering, verschillend representaties van hetzelfde

Ronde 3: Challenge in every topic: denken, probleem oplossing, redeneren, generaliseren, diepte voor versnellen. Niet meer van het zelfde, grotere getallen, snelheid in fluency verhogen (hoger dan nodig). Verbindingen leggen, interweaving, patroon herkenning, onderzoeken,

Ronde 4: Inside the x-box (fear/dislike algebra and how to overcome): patronen onderzoeken (samen), algebra laten zien als hulpmiddel om te generaliseren, curse of knowlegde (verwarring en misunderstanding van generalisaties) , taalgebruik, “algebra is de generalisatie van wat altijd waar is “, denken, betekenis geven

Ronde 5: Great tasks and where to find them: interweaving, denkvragen (andere oppervlakte, zelfde vaardigheid), wat is hier aan de hand, wat valt je op, wat herken je, fouten van anderen onderzoeken, diepte (richting begrip en concept) i.p.v. alleen moeilijker op inhoud.

Nu ik het zo op een rijtje terug zie en ik door mijn aantekeningen, oefeningen tijdens de workshops en de gemaakte foto’s van slides terug bladeren dan zie ik in bijna allemaal het volgende terug als een soort van rode draad en wellicht gekleurd ook door andere gedachten (ben het boek “Mathematical tasks – the bridge between teaching en learning”, door Chris McGrane en Mark McCourt aan het lezen) :

• Wiskunde is meer dan een opsomming van een lijst van vaardigheden en algoritmen kunnen uitvoeren, dat is misschien een basis om je werkgeheugen te ontlasten om waar het echt over gaan: kunnen kijken naar patronen, verbanden en relaties kunnen leggen, kunnen generaliseren, kunnen onderzoeken op (on) juistheden. Diepere kennis van een concept kan ook (wellicht niet altijd) het leren van de vaardigheid ondersteunen;
• Werken met patronen maakt een lage instap voor iedereen mogelijk (en dus ook succes), het creëert de kans / behoefte te generaliseren (algebra);
• Gedachtenloos rijtjes opgaven afwerken ontneemt de leerling de kans om echt te leren;
• De twee punten hierboven gaan een leerling nooit vanzelf doen: de juiste setting of cultuur (fouten maken mag/moet) , de juiste vragen stellen (geen antwoorden geven, maar vragen die het denken richten op wat van belang is), veel interactie tussen leerlingen onderling en leerlingen / klas – docent: het moeten verwoorden = denken!
• De huidige examen promoten echter nog (te) veel het tegenovergestelde: testen van vaardigheden en probleemoplossen in contexten die niet direct gericht zijn op diepte kennis van concepten en relaties. Daardoor krijg je onderwijs dat zich hierop richt, i.p.v. het ontwikkelen van de houding en ‘soft skills’ die horen bij een wiskunde denk- en werkhouding. Die kun je wellicht alleen mondeling testen of observeren ‘terwijl het plaats vindt’.

Als we echt aan de slag willen met het aan het denken krijgen van leerlingen dan moeten we goed helder hebben waarover we ze willen laten nadenken, en wat voor ons en de leerlingen nu de eerste stappen kunnen zijn om dat in ons curriculum op school en in combinatie met de gebruikte methode en planning kunnen gaan inbouwen. En stiekem willen we ook nog iets met gespreid en herhaald oefenen. Is die combinatie op te pakken in één keer : gaat het elkaar bijten inhoudelijk of bij ons zelf in onze ontwikkeling of kan het elkaar juist versterken. Daar nog maar eens goed over nadenken.

PS: vergeef me even alle layout foutjes, type foutjes en spellingsfoutjes: het was een overvolle dag en primaire doel was nu even mijn eigen gedachten ordenen. Storende fouten: geeft ze svp door dan pas ik het zsm aan.

Gedachten over ´Weer grip op je onderwijsresultaten ´

Twee weken terug las ik de blog ‘Weer grip op je onderwijsresultaten‘ van Karien Wijngaards op de site van Toetsrevolutie.

In de blog doet Karien een ‘aantal suggesties aan docenten die het lesgeven momenteel als ingewikkeld ervaren en teleurgesteld zijn over de leeropbrengsten van hun leerlingen. ‘ Ze noemt twee waarnemingen op verschillende scholen, namelijk dat er krampachtig wordt vastgehouden aan het curriculum zoals dat voor Corona was, met wat aanpassingen links en rechts. Daarnaast wordt er gesleuteld aan cijfers (en ik neem aan normeringen) om een gemiddelde op te trekken.

Tot de voorlaatste toets had ik zelf niet zo’n last van tegenvallende resultaten in mijn klassen. De laatste toets echter wel in mijn brugklas en mijn 2 havo groep; daar was ik ontzettend verrast (ondanks mijn intensief formatief handelen) over de prestaties bij de afsluitende toets. Navraag bij mijn leerlingen leerde dat zij vooral of zichzelf overschat hadden of de moeilijkheid onderschat. Beiden reken ik me aan, want als die onder- of overschatting er is, dan moet dat tijdens de lessen al ‘gewoon’ duidelijk worden. Voor hen, en voor mij. Feit blijft dat wat geleerd moest zijn, nu niet geleerd door de meesten. Bij beiden groepen is het een belangrijk hoofdstuk (met het oog op volgend schooljaar) dus het hier bij laten is geen optie.

De vijf tips die Karien geeft, die doe ik eigenlijk allemaal al, maar waar het nu met name knelt is de beschikbare lestijd die mijn klas en ik nog hebben.
Het curriculum dat we voor dit jaar voor ogen hadden hebben we gedurende het jaar al twee keer (fors) bijgesteld. We gaan nu ongeveer de lesstof ter orde grootte van 2 van de 8 hoofdstukken niet doen. Daarover hebben we afstemming gehad met leerjaar 3 om geen probleem in de doorlopende lijn naar komend schooljaar te creëren en dat lijkt op deze manier nog allemaal net goed te gaan.
We hebben besloten over een deel van het laatste hoofdstuk dan we gaan doen een SO te geven en in de afsluitende toets een combinatie te maken van dit laatste hoofdstuk en het hoofdstuk wat niet goed is gegaan.

Dat lijkt dus allemaal geen probleem te zijn en toch blijft dit wringen en voelt het niet goed.

Hoe dat komt? De focus ligt nu volledig (maar dan ook echt volledig) op vakinhoud en binnen de vakinhoud ook nog (bijna alleen) op de basis vaardigen en niet op de toepassing er van in een bredere context. De leerling leert nu een stukje wiskunde in isolatie en krijgt niet de mogelijkheid (tijd) om verbanden te leggen met andere gebieden het toe te passen in andere contexten en om het gereedschap als middel te leren gebruiken bij het oplossen van vraagstukken.
In een eerdere blog schreef ik over de doelen van wiskunde onderwijs:  “Een doel van het leren van wiskunde is het ontwikkelen van een wiskunde taal om jezelf in uit te drukken en om met die bril te kunnen nadenken.”

Daar kan ik nu niet of toch veel te weinig tijd aan besteden. Houd ik dan nog te krampachtig vast aan het curriculum? Kan ik in deze fase als individuele docent daar nog veel aan veranderen? Ik denk het niet.

Binnen de sectie hebben we al eens gesproken over een ´ui-model´ m.b.t. het kerncurriculum wat echt moet, een schil er om heen met wat ook belangrijk maar niet essentieel is. Daaromheen zit een schil wat wij als school en sectie belangrijk vinden en willen en dan als buitenste schil de persoonlijke wensen van de individuele docent.

Hierin zie ik twee aandachtspunten

1. Dit kunnen we niet als sectie alleen. Wiskunde is (ook) een ondersteunend vak en we moeten voorkomen dat wij vakinhoud niet of niet tijdig behandelen waar andere vakken dat (op een gegeven moment) nodig hebben. Er is ook een risico dat we denken: “oh, eenheden dat leren ze wel bij natuurkunde” of “procenten doet economie ook, dus dat hoeven wij niet te doen”. De samenhang van het totaal aan curriculum moet je schoolbreed afstemmen. Dat proces kost tijd, vraag flexibiliteit en een zorgvuldige afweging en planning.
2. De kans is groot dat we niet over één ui spreken, omdat we meerdere doelen nastreven dan alleen sec vakinhoud (en met name: vaardigheden) als curriculum te zien. Zoals ik al eerder verwees naar mijn vorige blog: er is zoveel moois te laten zien en laten ervaren over waar de wiskunde om ons heen is, hoe je wiskunde als een taal leert om die wiskunde in je omgeving te kunnen waarnemen, daar woorden aan te kunnen geven, over na te kunnen denken en vragen over te kunnen onderzoeken.

Deze twee aandachtspunten zijn (in mijn hoofd) te groot om daar in deze fase van het schooljaar nog zodanig handen en voeten aan te kunnen geven dat ons dat heel praktisch gezien gaat helpen de komende laatste 10 schoolweken van dit schooljaar. Wat het wel oplevert, is dat de noodzaak om als secties met elkaar binnen de school, en vervolgens binnen je eigen sectie een heel goed en schaalbaar beeld te vormen van het curriculum: wat willen we dat leerlingen leren?

De recent gepubliceerde Curriculumwaaier die SLO eind maart heeft gepubliceerd zou hier een bruikbaar instrument voor kunnen zijn om met elkaar dat gesprek erover aan te gaan en te komen tot een mooi samenhangend curriculum waarin we ook snel kunnen schakelen bij tijd te kort of tijd over. Alhoewel dat laatste voorlopig een droom blijft, ben ik bang.

Ik ben het volledig met Karien eens, dat je beter minder dingen goed kunt doen dan meer dingen en dat dan allemaal net niet. Daar wordt niemand blijer van. Echter dingen nu niet doen creëert een ander probleem voor de collega volgend schooljaar. Met het uitgangspunt: wat je doet goed doen is de keuze snel gemaakt. We doen minder en proberen dat zo goed mogelijk te doen.

Zonder een goed overwogen en afgestemd curriculum blijft het nu kiezen tussen twee kwaden. Wellicht dat ik het daar voor mezelf te moeilijk maak: het niet willen accepteren dat het nu niet anders is dan dit en dat in deze fase een goed overdachte keuze goed genoeg moet zijn. Voor nu. Ik vind dat lastig.

Over (wiskunde) onderwijs

De uiteindelijke trigger om deze blog te schrijven was het artikel van Koeno Gravemeijer in Didactief (maart 2022) over ‘Rekenen-wiskunde past niet in het model’. Met ‘het model’ wordt gerefereerd naar een trend in onderwijsland wat je generaliserend onderwijsonderzoek kunt noemen. Onderzoek wat leidt tot één onderwijsmodel waar voor alle vakken het beste onderwijs uit komt. Het artikel in Didactief is een verkorte versie van een longread die eerder op didactiefonline verschenen is. Door het inkorten van het artikel zijn er, in mijn ogen, wat nuances kwijtgeraakt en komt één en ander wat zwart – witter op mij over. En dat triggerde mij om wat gedachten die al langer in mijn hoofd dwarrelden eens op papier uiteen te zetten. Al was het maar om mijn eigen gedachten te ordenen.

Het begin van het artikel in Didactief.

Het vak past niet in een model

De eerste trigger was in de inleiding de zinsnede: ‘rekenen-wiskunde past niet in dit model’. Uitspraken van gelijke strekking heb ik wel vaker gehoord als ik ergens een training gaf over formatief werken : ‘Bij mijn vak kun je niet formatief toetsen’. Aan de andere kant, en dat blijkt wat meer uit de longread, heeft Gravemeijer zeker gelijk dat er in het onderwijs altijd een spanningsveld zit tussen onderzoek en de dagelijkse lespraktijk. Vaak wordt een model of een aanpak vanuit een onderzoek neergezet als ‘zo moet je het doen en dan komt het goed’. En dat is zelden het geval in de praktijk, om (zeker) twee redenen.

Ten eerste, als ik als docent een model of aanpak oppak en ga uitwerken dan ben ik op dat gebied en op dat moment een beginner. Ik maak daarin fouten, begrijp nog niet alle onderliggende principes en bij de uitvoering mis ik daarom belangrijke momenten om te handelen of maak ik keuzes die niet passen bij het model. Ik heb tijd nodig om me dit eigen te maken en het is nog maar de vraag of ik dat volhoud en doe, of dat ik besluit dat dit niet werkt voor mij en mijn klas.

Ten tweede, een klas is een dynamisch iets en is nooit hetzelfde. Er zijn zoveel factoren die een rol spelen, iedere dag weer. Hoe goed de lesvoorbereiding ook is: het loopt vaak toch net even anders. Ik moet improviseren, schakelen, meeveren, grenzen stellen op allerlei dimensies. Een model of een aanpak is een handvat, een houvast. Iets wat je op bepaalde momenten in je les kunt gebruiken. En soms dus ook niet. Het is het vakmanschap van de docent dat bepaalt welk instrument hij/zij op dat moment inzet. Er is dus niet iets als ‘zo moet het en dan komt het goed’ in alle omstandigheden.

Het artikel suggereert dat rekenen-wiskunde niet in het algemene model past. Ik denk dat we moeten oppassen dat we reken-wiskunde niet als de uitzondering positioneren: er zijn heel veel vakken, zo niet alle vakken, die je niet vanuit één model kunt aanvliegen of kunt vangen in één model.

Uitleggen en voordoen is niet de juiste aanpak

De tweede trigger was handvat nummer 4. ‘Leg denkwerk bij de leerling’. Daar ben ik het volledig mee eens: ‘Memory is the residue of thought’ (Daniel Willingham). Het is ook niet voor niets dat we in wiskunde de wiskundige denkactiviteiten hebben toegevoegd aan het curriculum. Wellicht dat daar de schoen wringt: gaat wiskunde überhaupt niet om denken en zou dat niet het primaire doel moeten zijn: leerlingen laten te denken als een wiskundige?

Dan komt de zin: ‘Uitleggen en voordoen is bij rekenen-wiskunde niet de juiste aanpak’. Ofwel: ik doe al ruim 14 jaar iets wat niet de juiste aanpak is. Dat is even slikken en geeft gelijk verwarring omdat ik (voor zover ik dan nu kan inschatten) goede resultaten boek daarmee. En verwarring omdat ik vanuit onderwijsboeken die ik lees toch vaak vormen of afgeleiden van Rosenshine principles of instruction tegen kom. 

In de longread staat wat meer toelichting over het model van horizontaal en verticaal mathematiseren (schematiseren). Kort gezegd gaat het daarbij om het vertalen van een probleem in context naar een wiskundige probleem, vervolgens binnen de wiskunde dit probleem oplossen en de resultaten terug te vertalen naar de context en daar te valideren.

Als je hier meer over wilt lezen dan zijn de publicatie Redeneren en formuleren bij wiskunde vakken (SLO, rond bladzijde 18) en een eerder artikel van Koeno Gravemeijer op Volgens-Bartjens aan te bevelen. 

Vanuit deze schematisering kan ik plaatsen dat uitleggen en voordoen (of voordoen en uitleggen?) voornamelijk op het gebied van de vaardigheden en dus oplossen van het geïdentificeerde wiskundige probleem het effectiefst is, maar dat bij het vertalen van context naar wiskunde (en vice versa) er een andere aanpak ‘beter’ is. In mijn lessen doe ik dat door met leerlingen te kijken naar overeenkomsten & verschillen, naar specifieke kenmerken, aanpak, strategie etc. Ik besteed daar best wat aandacht aan, en dus stelt dat me wat geruster en geeft deze uitspraak mij wat perspectief.

Mogelijke doelen van wiskunde onderwijs

Om hierop nog verder te reageren merk ik dat het voor mezelf nodig is om stil te staan bij het doel van rekenen-wiskunde onderwijs. Ik zie zelf daarin verschillende lagen of verschillende doelen.

• Om als burger goed mee te kunnen komen is een bepaalde mate van gecijferdheid nodig. Je moet om kunnen gaan met verschillende soorten verbanden, kunnen (hoofd)rekenen en een zeker getalbegrip hebben (deze opsomming is natuurlijk veel te kort en is niet uitputtend, maar gaat even over het algemene beeld).

• Wat ons als mensen bijzonder maakt is dat we kunnen denken (t.o.v. andere levende wezens). Wij kunnen denken omdat we een taal hebben waarin we ons kunnen uitdrukken. Wiskunde is daarmee ook een taal waarmee je leert kijken naar de wereld. Je ontkomt er niet aan dat je de afgelopen twee jaar naar de ontwikkelingen op Covid hebt gekeken met verschillende brillen op: aardrijkskundig, biologisch, globalisering, economische gevolgen, maatschappelijke aspecten, de verspreiding en groei van de besmettingen. Iedere bril vraagt een andere taal, een ander vocabulair, kijkt naar andere oorzaken/gevolgen en verbanden, doen andersoortige uitspraken over voorspellingen en verwachtingen. Wiskunde leren is het leren van een taal, het leren van kijken naar verbanden, het zoeken naar patronen, het doen van voorspellingen, het verklaren van wat je ziet. Een doel van het leren van wiskunde is het ontwikkelen van een wiskunde taal om jezelf in uit te drukken en om met die bril te kunnen nadenken.

• Bijna iedereen komt op een punt, binnen het leren van wiskunde, dat je worstelt. Je ziet niet gelijk de oplossing, je begrijpt een verband niet, je twijfelt over de aanpak die je nodig hebt. Bij wiskunde leer je daarom ook twee andere belangrijke persoonlijke aspecten
  • beginnen: misschien wat in het verlengde van doorzetten, maar deze zit nog een stap daarvoor. Ik merk dat veel leerlingen pas beginnen als ze de gehele aanpak (route naar het antwoord) overzien. Zien ze dat niet dan kunnen ze lang staren naar een stuk papier zonder dat er iets gebeurd. Wat ik mijn leerlingen leer is te kijken naar wat ze wel herkennen, wat ze wel al zouden kunnen doen, dat uit te voeren en dan opnieuw naar het geheel te kijken met de nieuwe informatie erbij. Ik leer ze schetsen maken, om tekst naar beeld te vertalen (de cognitieve load theory speelt hierin ook een rol, maar dat terzijde).
  • doorzetten: om een drempel over te komen leer je niet op te geven, leer je fouten te maken, leer je van je fouten te leren, leer je andere aanpakken te gebruiken, leer je hulp te vragen: kortom. Je ontwikkelt je doorzettingsvermogen.

Ergens aan beginnen en doorzetten zijn persoonlijke kwaliteiten, die een leerling niet alleen bij wiskunde leert, maar waar wiskunde wel een belangrijke bijdrage aan kan leveren, omdat het binnen dit vak praktisch iedere leerling overkomt.

• Wiskundige kennis en vaardigheden die noodzakelijk zijn bij het voorbereiden of aanleren van een beroep: in veel beroepen zul je een bepaalde mate van inhoudelijke wiskunde moeten kennen en kunnen. Die mate hangt af van je gewenste beroep en het niveau waarop je dat beroep of studie wilt uitvoeren/volgen. In het VO hebben we daarom de taak je daar zo goed mogelijk op voor te bereiden. Waarbij ik nog wel wil opmerken dat slechts een heel beperkt deel van de leerlingen een wiskundige studie gaan doen. Daarmee zeg ik dat we goed moeten nadenken over welke wiskunde we willen en moeten aanbieden aan welke leerlingen: niet voor iedere leerling is verregaande inhoudelijke wiskundige kennis nodig.

Misschien zijn er nog wel meer doelen te noemen van rekenen-wiskunde onderwijs, maar tot deze wil ik me nu even beperken. Gravemeijer heeft gelijk als hij de conclusie trekt dat het huidige dominante idee is dat we we nu zwaar inzetten op beheersen van procedures en dientengevolge het onderwijs zo inrichten dat de route daar naartoe zo efficiënt mogelijk verloopt. En ik denk dat Gravemeijer ook gelijk heeft dat heel veel wiskunde docenten daar van balen, omdat we daarmee voornamelijk het laatstgenoemde doel (en misschien het eerste doel ook wel voor een deel) hierboven nastreven en we niet toekomen aan de andere doelen: het laten denken als een wiskundige en de persoonlijke ontwikkeling. Van de meest gangbare wiskundemethodes in Nederland herken ik dit zeker bij Getal & Ruimte en Kern. Moderne Wiskunde geeft wat meer aandacht aan verwondering en (gestuurd denkend) ontdekken. De Wageningse methode daarentegen gaat uit van de denkende leerling, maar mijn ervaring daarbij is voor de meeste leerlingen een brug te ver is en behoorlijke docentsturing vraagt. Misschien gaat deze methode wel al uit van een een bepaalde aanwezigheid van wiskundig denken bij de leerling.

Onderwijs wat zich vormt naar de afsluitende toets

Dat we met z’n allen op het spoor van de procedures zitten is niet gek. Als je kijkt naar hoe een leerling na een aantal jaar zijn wiskunde schoolcarrière afsluit dan toetsen we toch voornamelijk procedures. Recentelijk zijn de wiskundige denkactiviteiten daar aan toegevoegd. We trainen leerlingen om een examen te kunnen halen, want daar staat of valt de vervolgstap van de leerling mee. De andere doelen die we nastreven zijn misschien moeilijk te meten, te kwantificeren of daar een norm op te zetten (als we dat al zouden willen): dus nemen we dat niet mee in de eindbeoordeling. Want laten we wel wezen: voor hoeveel leerlingen gaat het berekenen van een oppervlakte onder een kromme, of het berekenen van een hoek tussen twee balkjes van een bankje een bepalende rol spelen voor zijn/haar toekomst? Terwijl dat wel het enige is wat we meten en waarop we een beslissing nemen.

Terug naar de trigger: ’Uitleggen en voordoen is … niet de juiste aanpak’. Wiskunde is voor mij bij uitstek een vak waarin ik veel modelleer, veel hardop denk, voordoe en samendoe met leerlingen. Misschien is het ook wel omgekeerd: ik doe iets voor en leg uit wat ik doen, waarom ik iets doe etc. Het modelleren doe ik niet alleen op de wiskundige procedures, maar ook op aanpak, strategie, en metacognitie bij leerlingen. Mensen leren van observeren, van nadoen en imiteren. En ja dat geeft niet altijd gelijk ook het inzicht en begrip. Maar als je eenmaal iets kunt, wordt het wel makkelijker om daarover na te denken. Als ik wil dat leerlingen leren nadenken over iets, dan pas ik een efficiënte methode toe om de vaardigheid aan te leren, zodat ik tijd maak om met leerlingen te gaan denken wat we daar mee kunnen. Dus uitleggen en voordoen hebben zeker een functie. Echter niet uitsluitend.
Als we willen dat rekenen-wiskunde meer is dan door de hoepel van het CE te kunnen springen, dan moeten we met elkaar zorgen dat we het rekenen-wiskunde onderwijs anders organiseren en ook anders afsluiten voor leerlingen.

De genoemde triggers neem ik waar (en dat is mijn interpretatie) als fixed. Het lijkt andere aanpakken of gedachten uit te sluiten. Daar zit mijn allergie denk ik op: we sluiten iets uit, oordelen (in)direct over wat de ander doet.

Als ik het onderwijs iets gun dan is het wel om het vakmanschap bij de docent te laten. Voorzie die vakman van allerlei instrumenten die hem/haar daarbij kunnen helpen, waarbij het fijn is als bij het instrument ook gezegd wordt in welke omstandigheden of onder welke condities dat instrument het beste toch zijn recht kan komen. Maar laten we stoppen met prediken hoe het moet:

“Everything works somewhere; nothing works everywhere” (Dylan Wiliam)

Tom Sherrington heeft in een interessante blog geschreven over wat het betekent om evidence informed te werken. Kort gezegd: wees bewust van wat onderzocht is, ken de grenzen en beperkingen daarvan, blijf altijd kritisch en stem je onderwijs af op de situatie, de groep en het onderwerp.

Werken / leren met uitgewerkte voorbeelden

Wie bekend is met Craig Barton, zal ongetwijfeld ook gelezen hebben over ´worked examples´. Niet alleen schrijft hij er over in zijn boek, ook op zijn online platform kun je er een module over volgen.

Pas bij het lezen van het boek van Michael Pershan, Teaching math with examples kreeg ik een wat completer beeld van de mogelijkheden om ´uitgewerkte voorbeelden´ in te zetten in mijn lessen.
In een eerdere blog heb ik een kleine kijk gegeven in dat boek en benoem ik wat ik daar destijds uit heb gehaald voor mezelf.

Dit schooljaar ben ik voornamelijk met de volgende twee varianten aan de slag geweest.

Vind de fout en verbeter

Bij de ´vind de fout en verbeter´ opdrachten krijgt de leerling een aantal uitgewerkte opgaven, waarbij in iedere opgave (minstens) één fout zit. De leerling moet de fout vinden en dan diezelfde opgave maken zonder de fout (vandaar: verbeter de fout). Om de fout te vinden moet een leerling echt de aandacht focussen op iedere opgeschreven stap. De fout kan (zeker bij wiskunde) niet alleen in de inhoud zitten, maar ook in de notatie van de opgeschreven stappen in de uitwerking, wat maakt dat de leerling eigenlijk vanuit twee perspectieven moet kijken naar de uitwerking.

Ervaring leert dat de meeste leerlingen voornamelijk en als eerste kijken naar de inhoud, de wiskunde. Pas als ze daar niks kunnen vinden gaan ze naar de notatie kijken. Leerlingen die al wat zekerder zijn op het onderwerp en die meestal al bewust goede berekeningen opschrijven, zien sneller de aanwezige notatie fouten. Door op deze manier naar uitwerkingen te kijken, leren alle leerlingen te kijken op verschillende dimensies.

Kijken = denken, en denken = leren.

Omdat in je ééntje denken vaak lastig is, en je blik beperkt wordt door je eigen kennis en ervaring, laat ik deze opdrachten zo veel mogelijk in tweetallen maken.

Belangrijk is ook om altijd af te ronden met de juiste uitwerkingen. Dat kan door die uit te delen en ze zelf te laten kijken, maar dat kan ook door er een paar uit te halen waarvan je bij het rondlopen hebt gezien waar de meesten moeite mee hebben. Zelf nakijken en teruggeven kan ook, maar dat geeft jou werk en het ontneemt ook een extra leergelegenheid voor de leerling, of de mooie ontdekking van de leerling zelf dat ze hun succes zien.

letterrekeken-vind-de-foutDownload

lineaire-vergelijkingen-vind-de-fout-en-verbeterDownload

hoeken-en-symmetrie-vind-de-fout-en-verbeterDownload

Achterwaarts vervagen

In de Engelstalige literatuur spreekt men over backwards fading. Daar zijn een aantal interessante blogs over geschreven: hier in een blog van Tom Needham, hier een pagina van Craig Barton over worked examples en er is ook een doorloopje waarin dit terug komt.

Bij het achterwaarts vervagen geef je de leerlingen een volledig uitgewerkte voorbeeld als voorbeeld. Bij de vervolgopgave laat je de laatste stap weg, die moet de leerling dan aanvullen. En dat herhaal je bij de volgende opgaven: steeds laatst gegeven stap laat je weg tot de leerling de gehele uitwerking zelf moet maken. Je zou ook kunnen kiezen voor een aantal opgaven waarin steeds dezelfde stap ontbreekt, voordat je door gaat naar het weglaten van twee stappen, enzovoorts.

In het voorbeeld hierboven heb ik gelijk de laatste twee stappen weggelaten. Dat is een beetje tegenstrijdig aan wat ik erboven schreef. Het was een afweging vanwege de beschikbare ruimte op het blad en het kon ook omdat de laatste twee stappen uiteindelijk toch vaak in één regel opschreven gaan worden als de leerling wat verder in het leerproces is. Sterker nog, op het tweede blad van deze opdracht deden een aantal leerlingen dat gelijk al en hielden ze een lege regel over.

In mijn 2 havo klas heb ik dit jaar, veel meer dan voorheen, leerlingen die echt de stappen van de berekening ook tijdens het maken van hun (huis)werk al goed aan het opschrijven zijn, in nette stappen onder elkaar en die ook steeds een regel beginnen met het WAT ze gaan uitrekenen (de BC² en de BC in het voorbeeld hierboven). Doordat ze de stappen zo netjes opschrijven worden er ook veel minder fouten gemaakt in het berekenen van een rechthoekszijde (wiskundedocenten zullen direct begrijpen wat ik bedoel).

pythagoras-fading-2-havoDownload

Een paar voorbeelden waarbij je met uitgewerkte voorbeelden de aandacht van de leerling kunt richten. Op deze manier is het mijn leerlingen gelukt om veel gemaakte fouten te leren herkennen en daarop ook te acteren. Ook als ze daarna hun eigen werk aan het nakijken zijn, herinneren ze zich een gemaakte fout in één van de voorbeelden. Super mooi om te zien gebeuren.
De opdracht van achterwaarts vervagen was voor een leerling die was blijven zitten (en niet op dit specifieke onderwerp van wiskunde) wel vervelend. Dat verklaar ik door de expert die anders denkt dan de beginner en die geremd of belemmerd kan worden door een aanpak voor een beginner: het expertise reversal effect. Hier heeft Tom Needham ook een uitgebreide blog aan gewijd.

Al met al ben ik tevreden met de opbrengsten en hier ga ik in de loop van het jaar zeker nog een aantal werkbladen van maken samen met mijn collega´s.

Teaching Math with Examples – boek review

Nadat ik de podcasts van Craig Barton met Michael Pershan had beluisterd, heb ik het recente boek “Teaching math with examples” van Pershan gekocht en gelezen.

In de podcasts moest ik eerst even wennen aan de Amerikaanse stijl van Pershan, soms wat onnavolgbaar als hij hardop aan het nadenken is, maar al met al zat er genoeg in om mijn interesse in zijn boekje te wekken.

Craig Barton heeft van de podcasts overigens een tweeluik van gemaakt. De eerste podcast is eigenlijk niet van Craig zelf, maar is een gesprek tussen Ollie Lovell en Michael Pershan. De 2e podcast is daarna opgenomen en is wel tussen Barton en Pershan, wat een mooie verdieping op de eerste geeft.

Voordat je de podcast tussen Craig Barton en Michael Pershan gaat beluisteren kan het helpen om kennis te nemen van het model van een ‘Learning Episode’ dat Barton in zijn tweede boek (Reflect, Expect, Check, Explain) op blz 137 introduceert:

Dat schema kan wat overweldigend zijn als je deze voor het eerst ziet, maar van belang zijn (voor nu) twee zaken in relatie tot Teaching Math with Examples.

1. Als Barton het over worked examples (uitgewerkte voorbeelden) heeft dat zit dat voornamelijk in het blokje Example- Problem Pair. Dat zit aan het begin van het leren bij de fase van Uitleggen.
2. Daarnaast onderkent Barton in dit schema verschillende vormen van oefenen: Fluency, Intelligent en Purposeful, die ieder in een andere fase van het leren een rol spelen. Fluency bij het automatiseren, Intelligent om meer begrip te creëren en Purposeful wat meer toegepast is. In die stappen wordt ook de sturing van de docent steeds kleiner en neemt die zelfsturing van de leerling steeds meer toe.

Als Michael Pershan het over het werken met uitgewerkte voorbeelden heeft, dan bedoelt hij dat niet alleen in de begin fase bij het uitleggen. Voor hem, en dat beschrijft hij ook in zijn boek, passen uitgewerkte voorbeelden in de verschillende fasen van het leren.

Het boek van Pershan is niet zo groot, A5 formaat heeft 127 bladzijden en als je vertrouwd bent met uitgeverij John Catt, dan herken je het lettertype en stijl van opmaken.

Wat je merkt tijdens het lezen is de link die Pershan steeds heeft proberen te leggen tussen wat hij deed en wat nu doet en wat onderwijsonderzoek daarover tot nu toe kan vertellen. Wat hij daarover schrijft als laatste alinea in zijn boek is:

“…teaching cannot really be based in evidence, even if it is informed by it. We teachers need to be flexible in how we use what we read about.”

Door het boek heen geeft hij ook aan dat hij soms iets anders doet dan wat onderzoek aangeeft als wat mogelijk verstandig is om te doen, omdat hij in zijn setting met zijn class dan een andere afweging maakt. Dat geeft daarmee (voor mij) gelijk aan dat het een praktisch boek is: niet een theorie waar je zelf de vertaling moet maken naar je les, maar ‘met de voeten in de klei’. Ik houd daar wel van.

Na een introductie van hoe het leren met en van uitgewerkte voorbeelden werkt en een pleidooi over waarom dat een goede en effectieve manier van leren is, volgt in hoofdstuk drie de routine die hij toepast als hij werkt met uitgewerkte voorbeelden. Die routine bestaat uit vier stappen

1. Langzaam het uitgewerkte voorbeeld tonen;
2. Stilte geven voor leerlingen om dat te bestuderen;
3. Uitwisselen van gedachten tussen leerlingen onderling (denken-delen-uitwisselen) en daar specifieke vragen (door docent bedacht) over te stellen die de leerlingen moeten beantwoorden met elkaar;
4. De nieuwe inzichten toepassen in een nieuwe opgave.

Visueel komt dat samen in een eindplaatje wat er uit kan zien als :

Teaching math with examples, blz 48

In hoofdstuk vier gaat Pershan in een FAQ stijl in op veel gestelde vragen rondom zijn aanpak. Een aantal van die vragen had ik zelf inderdaad ook, dus fijn dat die gelijk beantwoord worden. In de volgende hoofdstukken schuift hij op naar het gebruiken van uitgewerkte voorbeelden bij probleemoplossing, bij feedback en naar het gebruik bij complexere vaardigheden zoals het leveren van een meetkundig bewijs.

Bij die latere hoofstukken werkt hij veel vanuit een hele taak gedachte. Om te voorkomen dat leerlingen te veel focus leggen op kleine deelstappen geeft hij aan dat het belangrijk is om te werken vanuit het hele plaatje. Leerlingen leggen daardoor makkelijker verbanden tussen de verschillende stappen die bij het uitwerken van een opgave horen.

Voorbeelden hoe hij dat doen:

• Achterwaarts vervagen (backwards fading): van een uitgewerkt voorbeeld laat je eerst de laatste stap weg, daarna de laatste twee etc.
• Vindt de fout: uitgewerkte voorbeelden waar een fout in zit. Met hulpvragen erbij om de aandacht te richten moet de leerlingen onderzoeken en achterhalen wat er waarom fout ging, en hoe het wel moet.
• Een (deels) uitgewerkt voorbeeld aanvullen: in de uitwerking ontbreekt ergens een deel of een regel, of sterker nog de uitwerking is volledig, maar welke vraag zou daar bij kunnen horen?
• Vergelijken: twee uitwerkingen laten zien, die beide kloppen waarbij leerlingen met gerichte hulpvragen gestuurd worden naar keuze van strategie: wanneer zou je welke aanpak gebruiken?

Als ik zijn manier van werken vergelijk met die van Barton dan valt me op dat ze in ieder geval gemeenschappelijk hebben: het richten van de aandacht van de leerling en het tijd geven aan de leerling om na te denken.

En toen ik me dacht bedacht, schoot me een model in gedachten wat ik eerder had gezien in het boek “Making every maths lesson count” (Emma McCrea):

Making every maths lesson count, blz 17

Zeker in de geest van “memory is the residue of thought” (Willingham) pas dit prima. De crux zit ‘m in waar je de aandacht op wilt richten en welke ondersteunende vragen je daar bij wilt stellen. Daar is voor een ervaren docent een stuk makkelijke dan voor een beginnende docent. Vanuit de ervaring ben je bekend met de veel gemaakte fouten en of misconcepties die leerlingen hebben bij een onderwerp. Daar maak je bij het werken met uitgewerkte voorbeelden namelijk veel gebruik van.

Al met al vond ik het fijn om even wat langer stil te staan bij het werken met uitgewerkte voorbeelden. In andere boeken is het een paragraaf en blijf ik wat hangen bij de gepresenteerde werkvormen. Met het verhaal er omheen wat Pershan geeft denk ik ook beter te snappen waarom dit kan werken, wat er voor nodig is om het te kunnen laten werken en op welke momenten en manieren ik dat zou kunnen doen.

Een mooie aanvulling dus op waar ik dit jaar wat meer mee bezig was: werken met grote overeenkomsten en kleine verschillen. Een aanpak die past bij de fase van Intelligent practise in het schema van Barton.

Wat ik in ieder geval mee neem (meer een bevestiging dan nieuw) is dat het richten van de aandacht van de leerlingen en die ergens over laten nadenken ontzettend belangrijk zijn om leerlingen in een leerstand te krijgen.

Mijn betere leerlingen zijn vaak meer producenten die de studiewijzer af willen krijgen. Dit soort denkopdrachten vertragen dat, en dat vinden ze vaak lastig, vervelend.

De wat zwakkere leerlingen, vinden nadenken over wiskunde niet leuk, vaak omdat ze zonder richting of ondersteuning hebben moeten nadenken en dan te weinig succeservaringen hebben opgedaan. Wat belemmert om wel te gaan nadenken.

Aan mij dus de taak om die leerstand aan te wakkeren en te ondersteunen.
Mijn didactisch repertoire is in ieder geval weer wat rijker geworden.

Succescriteria: aan de hand van eigen werk en dat van klasgenoten

De derde klas (vwo) is bezig geweest met gelijkvormigheid. Voor ze de stap maken naar de echt ingewikkelde opgaven, wil ik van een aantal dingen zeker zijn:

• Het opstellen van een verhoudingstabel en daarin rekenen met kruisproducten moet geen probleem meer zijn;
• Het correct opschrijven van de juiste stappen om te komen tot die verhoudingstabel moet bij iedereen vanzelfsprekend zijn

Met name het tweede doel is de focus van deze opdracht.

Wat leerlingen leren bij het aantonen en rekenen met gelijkvormigheid in de meetkunde (in dit geval driehoeken) is: redeneren, verbanden leggen, conclusies trekken, bewijs leveren en dat alles zodanig dat de hele bewijsvoering en redenatie stap voor stap te volgen zijn voor de lezer.

Ik heb de klas daarom de volgende opgave in de laatste vijftien minuten van een les laten maken:

(opgave komt uit Getal & Ruimte, 12 editie)

Zie het als een soort van exit ticket. Omdat de leerlingen tabellen moeten maken en bij hun notaties ook diverse wiskunde symbolen en notaties moeten gebruiken, heb ik er voor gekozen om de opdracht op papier uit te reiken en in te nemen. Het zou ook digitaal kunnen, maar er gaat dan teveel tijd verloren met de technische kant van het typen van die symbolen en notaties. Dat leidt te veel af.

Na de les heb ik door de gemaakte opgaven heen gebladerd, op zoek naar uitwerkingen van verschillende kwaliteit. Ik heb vooral gekeken naar de volledigheid en juistheid van het opschrijven van de uitwerking.  Van de negen geselecteerde uitwerkingen ben ik terug gegaan naar vijf in de stijl zoals je doet bij de werkvorm ‘My favorite No’.

Deze vijf heb ik in een google slide gezet in willekeurige volgorde met drie opdrachten erbij.

De slides heb ik via Google Classroom met ze gedeeld (voor iedere leerling een eigen exemplaar).

De drie opdrachten die ik daarbij gegeven heb zijn:

1. Sorteer deze opgaven (versleep de slides) van beste naar slechtste uitwerking
2. Schrijf op waar een goede uitwerking aan moet voldoen
3. Geef van één van de uitwerkingen aan hoe die verbeterd kan worden

In de volgende les zijn leerlingen in groepjes met elkaar in gesprek gegaan over wat zij goed vinden en wat niet of wat ontbreekt. Over wat ze duidelijk vinden, wat niet en waarom ze dat wel of niet duidelijk vinden. Zo zijn ze allemaal tot een volgorde gekomen en hebben ze beschreven wat er nodig is bij een goede uitwerking. Ze hebben daarna verbetertips opgeschreven voor één van de uitwerkingen.

Om te voorkomen dat de leerlingen nauwelijks verbeteringen hoeven te geven of misschien niet weten waar ze moeten beginnen met verbeteringen noemen als er nog erg veel moet verbeteren, kies ik ervoor om ze een uitwerking te laten verbeteren waar wel wat mee mis is, maar waar ook al veel goeds te zien is. Dat zorgt er voor dat ze echt op zoeken moeten gaan en de verbeteringen heel gericht moeten geven.

Leerlingen hebben zo een concreet en praktisch beeld van de succescriteria die horen bij een goede, volledige en navolgbare uitwerking. Gaandeweg het hoofdstuk hebben ze daar natuurlijk al mee gewerkt, maar deze opdracht pakt alles nog eens samen.

Nadat de leerlingen met de opdracht klaar waren, hebben we de door hen geformuleerd succescriteria nog samen besproken. Ik heb daardoor ook nog die succescriteria kunnen aanscherpen en de belangrijkste elementen ervan kunnen benadrukken.

Daarna heb ik ieder zijn of haar eigen uitwerking teruggegeven. Wat er gebeurde was erg mooi om te zien: zonder verder een opdracht te geven ging iedereen gelijk het eigen werk naast de succescriteria leggen en dat bespreken met de klasgenoot naast hem/haar.  Ze zaten zo in een focus van kritisch kijken naar ‘verbeteren’ dat de leergierigheid er vanaf spatte. 

Nadat de leerlingen in de les zelfstandig gewerkt hadden aan verdere opgaven heb ik als laatste, vlak voor het afsluiten van de les, de leerlingen nog gevraagd te kijken naar wat ze deze les opgeschreven hebben en hoe ze dat opgeschreven hebben, om ze te laten  controleren of dat voldoet aan de eisen. Willekeurig heb ik een aantal leerlingen bevraagd: wat doe jij al goed en waar moet je nog op letten.

Tijdens de les heb ik waardevolle en leerzame gesprekken gehoord, met mooi (of soms nog zoekend) wiskunde taalgebruik. Tijdens de afsluiting wist iedere leerling die ik sprak concreet te benoemen wat er goed gaat in het eigen werk en waar op gelet moet worden.  Na de les heb ik de slides snel vluchtig bekeken om te zien of er bijzondere dingen opvielen. Wat me in ieder geval opviel is dat niet alle leerlingen een volledige beschrijving hadden gegeven van waar een goede uitwerking aan moet voldoen. Vanuit de klassikale bespreking die we hadden na de uitvoering van de opdracht had ik wellicht nog de leerlingen de uiteindelijke versie van succescriteria in hun schrift kunnen laten schrijven. Daarmee gaat iedere leerling dan naar huis met de juiste versie daarvan.

Inmiddels heb ik de toets nagekeken, waarbij ik slechts bij één leerling constateer dat de notatie niet op orde is. Ik zie wel dat de juiste structuur en juiste stappen er staan, maar het is niet de formele wiskunde taal. Eén andere leerling heeft een aantal keer conclusies getrokken zonder aan te tonen hoe hij/zij daar aan gekomen is. 

Al met al een mooie combinatie van comparative judgement, succescriteria opstellen, exit tickets, (peer)feedback en reflectie. Het exit ticket maken kostte mij 6 minuten. Printen en kopiëren: 1 minuut.  De uitwerkingen filteren, vijf stuks fotograferen en in een slide zetten: 12 minuten. De slide klaar zetten in classroom: 1 minuut. Al met al dus 20 minuten. Voor een les van 60 minuten. 

Wie is er aan het werk geweest? De leerling! En dat zonder een administratie bij te houden. 

Wederom dank aan Bram en Melle voor het meelezen, de feedback en de aanscherpingen!

Formatief toetsen & Onderwijs op afstand – hoe doe ik dat nu?

De afgelopen twee weken heb ik regelmatig de vraag gekregen: “Jörgen, jij doet veel met formatief toetsen, hoe doe je dat nu online en heb je nog tips voor goede digitale toetsprogramma’s?”

bron afbeedling: https://www.gynzy.com/nl/start/stappenplan-onderwijs-op-afstand/

Een eerlijk gezegd wist ik niet zo goed hoe deze vraag te beantwoorden. Mijn koorts en hoesten hielpen in deze fase ook niet mee om scherp  na te denken. Ik heb de eerste week dus wat meer vanaf de zijlijn meegekeken en pas in de tweede week ben ik actiever om me heen gaan kijken wat er allemaal gebeurde en hoe ik die gestelde vraag nou ga beantwoorden.

Wat ik zie gebeuren om me heen varieert tussen uitersten. Aan de ene kant een docent die aangeeft wat er over drie weken allemaal af moet zijn en aangeeft vragen per mail te beantwoorden. Tot een docent die al zijn lessen nog steeds geeft, nu online. Daarbij zoekende is naar de beste tooling, allerlei websites inzet, dagelijks alle leerlingen appt/contact zoekt en er alles aan gelegen is om het leren zo goed en kwaad als het kan te willen begeleiden.

Er zijn talloze blogs inmiddels verschenen over o.a. Microsoft Teams, Google Hangout Meet en Zoom. Vaak nog gericht op de technische inzet ervan, en nog wat minder op de didactiek en kwaliteit van de les. Onder het mom (heel logisch) van we willen contact met onze leerlingen: hoe doen we dat. Super belangrijk in deze fase. Dit is ook mijn eerste prioriteit.

Ik zie ook veel vragen voorbij komen over “Hoe toets je nou op afstand en hoe kun je dat betrouwbaar doen?” De bekende online toets programma’s passeren de revue en er wordt gebrainstormd over het in beeld brengen van het toetsafname moment (proctoring) om die betrouwbaarheid te verhogen.

Als het gaat om die betrouwbaarheid merk ik dat ik daar wat op afhaak. Mijzelf hardop afvragend hoe dat nou komt, kom ik uit op dat ik niet in formatief toetsen denk maar in formatief handelen. Sinds ik formatiever ben gaan werken, ben ik misschien ook wel meer (kortere) interactieve instructies gaan geven. Ik ben constant op zoek naar of en hoe het onderwijs is aangekomen bij de leerling en wat dat voor de vervolgstap (van de leerling of mij ) betekent. In een diagloog met de klas en veel vragen stellen gaat dat inmiddels als vanzelf.  Ik kan dat nu niet in een digitale toets afvangen, dat voelt namelijk veel te laat: niet meer tijdens het leren maar pas daarna.  En hoe geef je een individueel vervolg n.a.v. de resultaten van zo’n toets , op afstand? Betekent dat differentieren in studiewijzers?  In aparte uitleg momenten voor de verschillende soorten fouten die leerlingen maken? Ik weet dat nog niet zo goed, en ben daar net als iedereen zoekende in.

Wat doe ik nu dan wel?

• We hebben er voor gekozen om nu (voorlopig) alleen met algebra verder te gaan in klas 1, in kleine stapjes. Dat heeft o.a. als reden dat we sinds dit schooljaar het Engelstalige programma Blutick gebruiken. Dat lijkt wat op Algebrakit en bevat fijn oefenmateriaal voor algebra . Leerlingen kunnen hier veel online op oefenen en krijgen bij foute antwoorden directe feedback (soms rijk, bij bekende fouten, soms gewoon de melding : fout) en kunnen dus geen foute manieren inslijpen per ongeluk, wat wel zou kunnen bij vragen op papier, zonder die terugkoppeling.
• We bieden een uitleg video aan (veelal Wiskundeacademie) die we in Edpuzzle een beetje bijknippen en waar we wat vragen in stellen tijdens het moeten bekijken. Dat zorgt voor een actievere kijken en luister houding bij leerlingen en het voorziet mij al vroegtijdig de denkpatronen van leerlingen.
• Na de uitleg gaan leerlingen oefenen in Blutick. Ik zie hun antwoorden als ik daarop inzoom, zie wie er moeite mee hebben, dus ik kan hier gericht ook vragen stellen of hulp aanbieden.
• Na het online oefenen maken de leerlingen een werkblad (gemaakt via Wiskunjetrainen.nl) om hetzelfde nog eens op papier te doen en zelf na te kijken. Op papier, zonder direct feedback krijgen,  is echt fundamenteel anders voor leerlingen, plus dat ze door het schrijven een andere aanspraak op hun brein moeten doen.
• Na het oefenen maken ze een controle blad met een paar vragen (ook gemaakt via Wiskunjetrainen) die ze moeten inleveren in classroom, die ik nakijk, waar ik feedback op geef  en waarvan zij de feedback moeten verwerken.
• Ik geef nu één online les (conform afspraken op school, ik vermoed dat dat er meer worden) waarbij ik de belangrijkste punten en fouten aanstip. En dan oefenen we even samen. Ik zet de opgave op het digitale bord (gedeeld scherm in Google Hangout Meet) en zij geven hun antwoord via het digitale wisbordje in GoFormative. Ik zie gelijk welke antwoorden zij geven en pas mijn uitleg of vervolg vraag daarop aan. Tot nu toe werkt dat naar behoren. Ik bewaar hier geen resultaten van leerlingen: wat zij schrijven is op dat moment informatie voor mijn les. Namen van leerlingen waarvan ik zie dat ze er moeite mee hebben, schrijf ik even apart op om later specifiek te kunnen begeleiden/ buiten de les vragen te stellen etc.
• Ik ga komende week ook digitale quiz programma’s inzetten. We hebben als collega’s eerder dit jaar gekozen voor het programma Quizalize.
  In dit quiz programma wil ik dat leerlingen een aantal dingen gaan automatiseren, om te beginnen met
  • Wortels en kwadraten van de getallen 1 t/m 20
  • Het omzetten van (veelvoorkomende) breuken, decimale getallen, percentages van en tussen elkaar
  • Rekenen met negatieve getallen (eenvoudige sommen, om de rekenregels er goed in te krijgen)
  • Van die quizjes ga ik niet zo veel bijhouden (het programma doet dat wel), maar voor mij zijn al die resultaten nu nog niet zo van belang. Ik vind het belangrijk dat leerlingen blijven oefenen en merken dat ze beter worden. Ik zal ze dus wel aanspreken en aansporen om te oefenen, maar de resultaten: dat is aan hen. En daarmee vervalt gelijk ook de noodzaak voor betrouwbaarheid: zij doen dit voor zichzelf, worden niet afgerekend op het resultaaat (maar wel aangesproken op het doen).

 

Al met al best wat ICT inzet, maar alles met een specifieke functie en toegevoegde waarde. Voor mijn leerlingen is alleen de online les via Hangout Meet nieuw. Alle andere programma’s waren al in gebruik. Dat scheelt enorm: geen opzet of opstart problemen.
En zo gaan we komende paar weken in, wellicht evolueren we verder met elkaar. En tot die tijd mis ik de leerlingen, mijn collega’s, het echte contact, de directe interactie, het geven van een knipoog en dat soort dingen.